From the figure we note that the angles a and (6x-5) are vertically opposite, then they are equal. Furthermore tha angles a and b are also equal since they are alternate interior angles. From this we conclude that
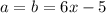
Once we know that, we see that the angles (7x-10) and b are supplementary then their sum should be 180. From those arguments we have the equation
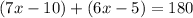
Solving for x, we have
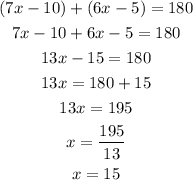
Then x=15 degrees.