Question

Hi someone please help me and thanks have a great day.Hi someone please help me and thanks have a great day.Hi someone please help me and thanks have a great day.Given EFG shown below, state the value of the missing angle

Answer 1

Answers:

m∠G = 59.49

m∠E = 30.51

Step-by-step explanation:

To know the measure of the angles we will use the trigonometric function sine. So, sin G can be calculated as:

`\sin G=\frac{Opposite\text{ side}}{Hypotenuse}`

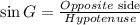
Where the opposite side of ∠G is FE and the hypotenuse is GE, so replacing the values, we get:

`\begin{gathered} \sin G=(FE)/(GE) \\ \sin G=(56)/(65) \end{gathered}`

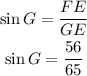
So, using the inverse function of sine, we get that the measure of angle G is:

`\begin{gathered} \sin G=0.86 \\ G=\sin ^(-1)(0.86) \\ G=59.49 \end{gathered}`

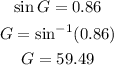
In the same way, the sine of angle E is equal to:

`\begin{gathered} \sin E=\frac{\text{ Opposite side}}{Hypotenuse} \\ \sin E=(GF)/(GE) \\ \sin E=(33)/(65) \end{gathered}`

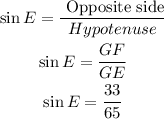
So, solving for E, we get:

`\begin{gathered} \sin E=0.51 \\ E=\sin ^(-1)(0.51) \\ E=30.51 \end{gathered}`

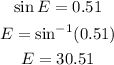
Therefore, the answers are:

m∠G = 59.49

m∠E = 30.51