ANSWER
![y=2x^2+8x+12;[-5,-1]](https://img.qammunity.org/2023/formulas/mathematics/college/9eaaeo0q8kz8grlndia9mac43lbtwt5psz.png)
Step-by-step explanation
We want to find the rectangular form of the given parametric equation:
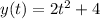
on the interval [-3, 1] where:
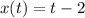
To do this, first, write t in terms of x:
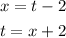
Now, substitute the expression for t into the given equation and simplify:
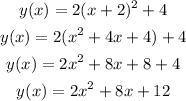
That is the rectangular form.
To find the interval (x1, x2), we have to substitute the values of the boundaries of the interval (t1, t2) = [-3, 1] into the equation for x:
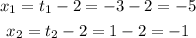
Hence, the interval is:
![[-5,-1]](https://img.qammunity.org/2023/formulas/mathematics/college/bc15p6bcpbvjy4gikvpwhdqwz3ltbup00w.png)
That is the answer.