1 Answer

Martin Pilch · Answer 1 · 2023-07-25T21:15:06+0000

Answer:

1i) P(A) = 1/2

ii) P(B) = 1/2

iii) P(A and B) = 1/4

2) P(A) + P(B) - P(A and B) = 3/4

3) P(A or B)/ P(A U B)

Probability is the likelihood or chance that an event will occur. Mathematically;

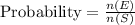
$\text{Probability}=(n(E))/(n(S))$

n(E) is the number of events

n(S) is the total sample space

An 8-sided die with faces labeled 1 to 8 will be rolled once, the sample space will be S = {1, 2, 3, 4, 5, 6, 7, 8}

n(S) = 8

a i) For event A, we need to get the number of outcome greater than 4.

A = {5, 6, 7, 8}

n(A) = 4

P(A) = n(A)/n(S)

P(A) = 4/8 = 1/2

ii) For event B, we need the outcomes that gives an even number.

B = {2, 4, 6, 8}

n(B) = 3

P(B) = n(B)/n(S)

P(B) = 4/8 = 1/2

iii) For the probability of the event of rolling a number greater than 4 and rolling an even number,

P(A and B) = P(A) * P(B)

P(A and B) = 1/2 * 1/2

P(A and B) = 1/4

2) To compute P(A) + P(B) - P(A and B), we will substitute resulting probabilities in (a) into the expression as shown:

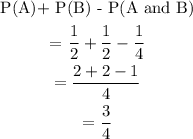
$\begin{gathered} \text{ P(A)+ P(B) - P(A and B) } \\ \text{= }(1)/(2)+(1)/(2)-(1)/(4) \\ =(2+2-1)/(4) \\ =(3)/(4) \\ \end{gathered}$

Hence P(A) + P(B) - P(A and B) = 3/4

3) Note that P(A and B) can also be written as P(A n B) and according to set theory;

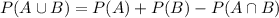
$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

This can be also be expressed as:

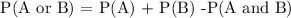
$\text{ P(A or B) = P(A) + P(B) -P(A and B)}$

Hence from these two notations, we can see that the answer that makes the equation true is P(A or B)/P(A U B)