Question

Suppose that y varies inversely as the square of x, and that y = 9 when x = 15. What is y when x 2? Round your answer to two decimal places if necessary.

Answer 1

Y varies inversely as the square of x. This relationship can be expressed as

`y=(k)/(x^2)`

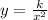
where k is a constant. we need to find the value of k

To do that, we use the provided data, y = 9 when x = 15. Substituting in the above equation:

`9=(k)/(15^2)`

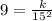
Solving for k:

`k=9\cdot15^2=2,025`

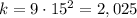
The equation is, then:

`y=(2,025)/(x^2)`

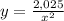
We finally need to find the value of y when x = 2:

`y=(2,025)/(2^2)=(2,025)/(4)=506.25`

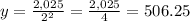
y is 506.26 when x = 2