Let,
x = Maps sold
y = Profit
a.) Since the graph shows it's linear, let's create an equation applying this formula,
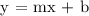
From the graph, let's use the ordered pairs (40, 0) and (0, -200) from the given data,
Let's solve for m,
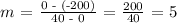
Let's solve for b, let's use (40,0) for x and y.
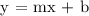
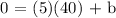
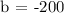
Thus, the equation will be,
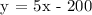
Or we can rephrase it as an equation to solve for the profit,

b.) The ordered pairs (40, 0) and (0, -200) represents Brian's profits from selling a different number of maps.
(40, 0) = Brian will get no profits if he'll only sell 40 maps. His sale will only be just breakeven to his initial expenses.
(0, -200) = Brian will lose $200 which is his initial expense if he couldn't sell a map.
c.) Brian's profit if he sells 300 maps.
Let's use the formula we made from Part. a,
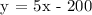
x = 300, we get,
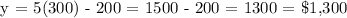
Brian will earn $1,300 dollars if he sells 300 maps.