If you have atriangle with sides a, b and c and internal angles A, B and C
One side of a triangle is less than the sum of the other two sides and greather than their difference:
![\begin{gathered} \\ ca-b \\ \\ a-bSides:<p>a=21cm</p><p>b=16cm</p>[tex]\begin{gathered} 21-16The internal angles in a triangle sum 180º[tex]A+B+C=180º]()
A=82º
As this is an obtuse triangle, the angle A is the angle with greater measure, then the opposite side of this angle will be the side with greater measure.
The opposite side to angle A is a, then:
![5The internal angles of a triangle sum 180º:[tex]\begin{gathered} 82º+B+C=180º \\ B+C=180-82 \\ B+C=98º \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/95czusevwgui4jmcwu0d1td3irflxo4dsf.png)
The relation between the angles and the sides in a triangle:
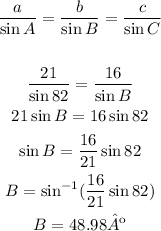
Angle B is 48.98º
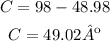

As you can see the given data allow you to find an exact measure for the other side and angles in the triangle.
Then, as you can see, you can just form one triangle with A=82º, a=21cm b=16cm