Question

Graph the solution set of the following linear inequality answer the questions on the bottom

Answer 1

Given the inequality:

`-6x\ge-6y+54`

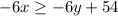
Divide all through by 6:

`\begin{gathered} (-6x)/(6)\ge(-6y)/(6)+(54)/(6) \\ -x\ge-y+9 \end{gathered}`

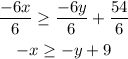
(a)The inequality sign is greater than or equal to, therefore, the boundary line is solid.

(b)Next, we draw the boundary line using the boundary line equation: -x=-y+9

`\begin{gathered} \text{When }x=0,-0=-y+9\implies y=9\implies(0,9) \\ \text{When y}=0,-x=0+9\implies x=-9\implies(-9,0) \end{gathered}`

Two points on the boundary line are (0,9) and (-9,0).

(c)The graph is attached below:

Note: To determine