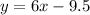Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into thecorrect position in the answer box. Release your mouse button when the item is place. If you change your mind. dragthe item to the trashcan. Click the trashcan to clear all your answers,Indicate the equation of the given line in standard form.The line that is the perpendicular bisector of the segment whose endpoints are R(-16) and S(5.5)

Answer 1

The process we will follow to find the solution will be to first find the slope between the two given points, then apply a condition to find a perpendicular slope, and finally, we will find the equation of the perpendicular bisector line.

Step 1. Find the slope between the points R and S.

The points R and S are as follows:

`\begin{gathered} R(-1,6) \\ S(5,5) \end{gathered}`

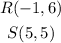
We will label these points as follows:

`\begin{gathered} x_1=-1 \\ y_1=6 \\ x_2=5 \\ y_2=5 \end{gathered}`

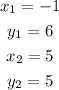
And we need to find the slope "m" using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Substituting our values and solving the operations:

`\begin{gathered} m=(5-6)/(5-(-1)) \\ m=(-1)/(5+1) \\ m=(-1)/(6) \end{gathered}`

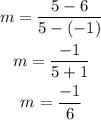
The slope between R and S is m=-1/6

Step 2. We need to find a line that is the perpendicular bisector of the segment R to S. We will call the slope of this perpendicular line

`m_p_{}`

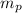
And use the following condition for the slopes of two perpendicular lines:

`m\cdot m_p=-1`

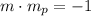
From this it follows that:

`m_p=(-1)/(m)`

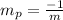
Where m is the slope we found in step 1:

`m_p=(-1)/(-(1)/(6))`

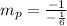
Solving this division we find the slope of the perpendicular line:

`\begin{gathered} m_p=(6)/(1) \\ m_p=6 \end{gathered}`

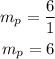
Step 3. We have the slope of the perpendicular line, but, to be a perpendicular bisector, this perpendicular line needs to pass through the midpoint between R and S.

Calculate the midpoint between R and S using the following formula:

`((x_1+x_2)/(2)_{},\frac{y_1+y_2_{}}{2})`

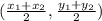
Substituting the values for x1, x2, y1, and y2 that had in step 1:

`((-1+5)/(2),(6+5)/(2))`

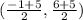
solving the operations:

`((4)/(2),(11)/(2))`
`(2,5.5)`

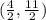
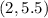
The midpoint is at (2, 2.5).

Step 4. At this point we know the slope of the perpendicular bisector line:

`m_p=6`

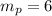
And we also know that it has to pass through the midpoint:

`(2,2.5)`

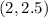
The next step is to label the coordinates of the midpoint for reference:

`\begin{gathered} x_0=2 \\ y_0=2.5 \end{gathered}`

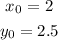
And use the point-slope equation:

`y-y_0=m_p(x-x_0)`

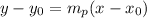
Substituting in this equation the known values:

`y-2.5=6(x-2)`

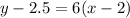
And to have this equation in standard form we need to solve for y:

`y=6(x-2)+2.5`

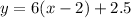
We can simplify by using the distributive property on the right-hand side of the equation:

`\begin{gathered} y=6x-12+2.5 \\ y=6x-9.5 \end{gathered}`

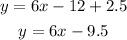
The equation of the perpendicular bisector line in standard form is:

`y=6x-9.5`

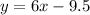
Answer:

`y=6x-9.5`