Question

What is the expected value of the probability distribution of the discrete random variable X?xP(X = x)2.074.196.258.1110.0712.3014.01

Answer 1

`E(x)=\mu=7.72`

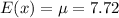
Explanations:

The formula for finding the expected value of a probability distribution is expressed as:

`E(x)=\mu=\sum xP\mleft(x\mright)`

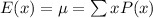
Substituting the values in the table into the formula will give:

`\begin{gathered} E(x)=2(0.07)+4(0.19)+6(0.25)+8(0.11)+10(0.07)+12(0.30)+14(0.01) \\ E(x)=0.14+0.76+1.5+0.88+0.7+3.6+0.14 \end{gathered}`

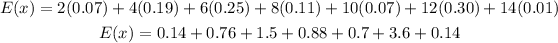
Taking the resulting sum of to get the expected value;

`E(x)=\mu=7.72`

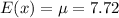
Hence the expected value of the probability distribution of the discrete random variable X is 7.72