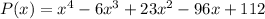Question

Give an equation with integer coefficient for the quartile polynomial with given roots below:

Answer 1

For a polynomial with real coefficients, if one root is complex, another root is the conjugate of it. So here we have that one root is x=-4i, so another root will be x=+4i.

Also, with roots we have that the square root of a number has a positive and a negative result. So, if one root is x = 3 - sqrt(2), then another root is x = 3 + sqrt(2).

We know that we can write a polynomial like:

`P(x)=(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

Where x1, x2, x3, x4 are the roots. So for this problem we have:

`P(x)=(x-4i_{})(x+4i)(x-3-\sqrt[]{2})(x-3+\sqrt[]{2}_{})`

If we solve the multiplication we get the polynomial:

`P(x)=(x^2-(4i)^2)((x^{}-3)^2-(\sqrt[]{2})^2)`

What I did there is a difference of two squares with the first two binomials and the second two binomials. Now we solve the squares:

`P(x)=(x^2+16)(x^2-6x+9-2)`

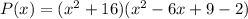
And do the final distribution to get our polynomial:

`P(x)=x^4-6x^3+7x^2+16x^2-6\cdot16x+7\cdot16`

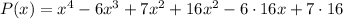
And solve:

`P(x)=x^4-6x^3+23x^2-96x+112`