Let's suppose that we have the following function in standard form:
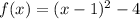
We know that the general standard form of a function is:

then, in this case we have the following:
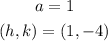
Since the function is quadratic, the graph will be a parabola. The point (h,k) is where the vertex is located on the plane.
Then, we can find the roots of the function to see where the intersections with the x-axis are (if there are any):
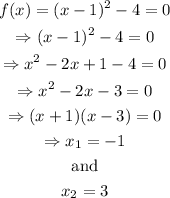
we have that the parabola will cross the x axis when x=-1 and x=3, then, a sketch of the graph of f(x) would look like this: