We are asked to determine the possibility of getting heads and getting blue from the spinner. This is represented as:

Since we have the probability of two independent events happening at the same time the probability is the product of the probability of both each event, like this:

Now, we will determine each of the probabilities. We begin with the probability of getting head. The probability is the quotient between the desired events, in this case, 1 (heads), and the number of possible events, in this case, 2 (heads, tails). Therefore, the probability is:
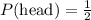
Now, we determine the probability of getting blue. The number of desired events is 1 (blue) and the number of possible events is 3 (blue, white, gray), therefore, the probability is:
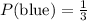
Now, we substitute in the formula for the combined probabilities:
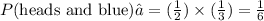
Therefore, the probability of getting heads and blue is 1/6.