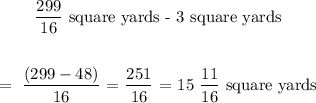The area of the wall not covered by the three posters is 15 11/16 square yards
We are interested in calculating the area of the wall not covered by the 3 posters.
To go about this, we need to know the area of the wall, afterwards, we are going to calculate the area of the wall taken by the posters.
To calculate the area of the wall taken by the posters, we subtract the area of the posters from the area of the wall.
From the question, we can see that the shapes of both the wall and posters are rectangular.
Mathematically, we can calculate the area of the wall as follows;
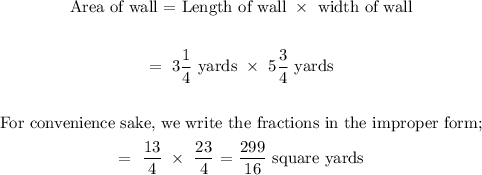
From here, we proceed to calculate the area of the posters;

So the area of the wall not covered by the posters will be;