In account A:
1.
Mr. Malone is putting $200 first, then he deposits $15 each month
Since y is the total amount of money after x months, then
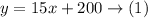
In account B:
2.
Mr. Malone is putting $300 first, then he deposits $10 each month
Since y is the total amount of money after x months, then
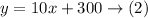
3.
We will subtract equation (1) from equation (2) to eliminate y
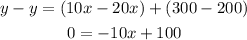
Add 10x to each side
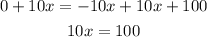
Divide both sides by 10
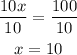
Substitute x by 10 in equation (1) OR (2) to find y
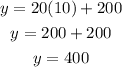
The solution of the equations is x = 10, y = 400
4.
After 10 months the accounts will have the same balance
5.
The balance will be $400