Question

Math 3 Literacy ReviewLine A and Line B are increasing at constant rates. The initial height of Line A is 2 feet. The initial height of Line B is 3 feet. The height of A after x = 1 (or 1 minute) is 6 feet. The height of B at x = 1 (or 1 minute) is 3 1/2 feet.What will be the height in feet of each line at x = 4 (after 4 minutes)? Give a mathematical explanation including each line's constant rate and how you arrived at your conclusion. Write your answer in complete sentences and show work.

Answer 1

We know that

• The initial height of Line A is 2 feet.

,

• The initial height of Line B is 3 feet.

,

• The height of A after 1 minute is 6 feet.

,

• The height of B at 1 minute is 3 1/2 feet.

For Line A, we can express two coordinate pairs (0,2) and (1,6).

For Line B, we can also express two coordinated pairs (0,3) and (1, 3.5).

Using the coordinated pairs, we can find the rate for each line using the slope formula.

`m=(y_2-y_1)/(x_2-x_1)`

Applying the formula for each line, we have

`\begin{gathered} m_A=(6-2)/(1-0)=(4)/(1)=4 \\ m_B=(3.5-3)/(1-0)=(0.5)/(1)=(1)/(2) \end{gathered}`

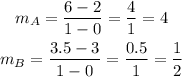
• The rate of Line A is 4 feet per minute.

,

• The rate of Line B is 1/2 feet per minute.

Once we have the rate of each line, we can form a slope-intercept equation for each of them using the slope-intercept formula.

`y=mx+b`

Where b is the initial condition. For Line A, b = 2. For Line B, b = 3. So, the equations are

`\begin{gathered} A\colon y=4x+2 \\ B\colon y=(1)/(2)x+3 \end{gathered}`

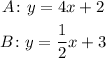
Once we have the equation for each line, we have to evaluate them when x = 4 (after 4 minutes).

`\begin{gathered} A\colon y=4(4)+2=16+2=18 \\ B\colon y=(1)/(2)(4)+3=2+3=5 \end{gathered}`

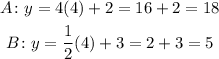
Therefore, Line A's height, after 4 minutes, is 18 feet, and Line B's height is 5 feet.