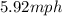
1) We can solve this problem, by considering that we are dealing with ratios. So let's start out writing the equation keeping in mind this relation:
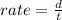
2) So, we can write out this keeping also in mind that Kerrie goes upriver and down the river:

We can discard negative values for the rate. Then the rate in still water is 5.9 mh