Question

Part B onlyThe braking distance d, in meters, of a vehicle traveling at a velocity v, in meters per second, is given by the formula

Answer 1

340 feet

Explanation:

The braking distance​ d, in​ meters, of a vehicle traveling at a velocity​ v, in meters per​ second, is given by the formula:

`d=(v^2)/(2\mu g)`

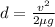
Part B

Given:

• v =68 mi/hr

,

• μ = 0.45

,

• g = 9.8 m/s²

First, convert the velocity, v from miles per hour to meters per second.

• 1 miles = 1609.34 meters

,

• 1 hour = 3600 seconds

`68(miles)/(hour)=68*(1609.34)/(3600)(meters)/(seconds)=30.40\text{ meters/seconds}`

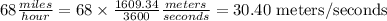
Substitute v=30.40 m/s into the formula.

`\begin{gathered} d=(30.40^2)/(2*0.45*9.8) \\ d=104.78\text{ meters} \end{gathered}`

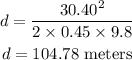
Finally, convert the result to feet.

`\begin{gathered} 1\text{ meter}\approx3.28\text{ feet} \\ \implies104.78\text{ meters}=104.78*3.28\text{ feet} \\ =343.6784\text{ feet} \\ \approx340\text{ feet \lparen rounded to the nearest ten\rparen} \end{gathered}`

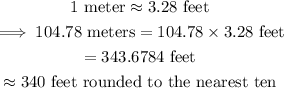
The braking distance is about 340 feet.