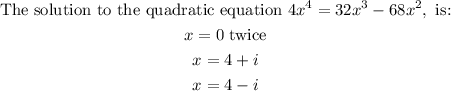Answer
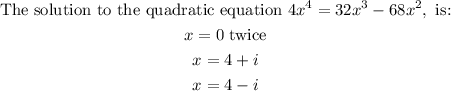
SOLUTION
Problem Statement
We are asked to find the real and imaginary solutions to the following equation:
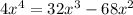
Method
- To solve this question, we should follow these steps:
1: Move all the terms to one side
2. Factorize the x-squared term since it is common to all the terms
3. Equate the factorized terms to zero. and find the real roots from the x-squared term
4. Solve the other quadratic equation and find the imaginary roots. Here we shall apply the Quadratic formula. The Quadratic formula is given as:
![\begin{gathered} \text{Given the quadratic equation:} \\ ax^2+bx+c=0 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pj85ai4y72qol8hj77ygfstwo43fcwhehr.png)
Solution
![\begin{gathered} 4x^4=32x^3-68x^2 \\ 1\colon\text{Move all the terms to one side} \\ 4x^4-32x^3+68x^2=0 \\ \\ 2\colon\text{Factorize the x-squared term out since it is common to all the terms} \\ x^2(4x^2-32x+68)=0 \\ \\ 3\colon\text{Equate the factorized terms to zero.} \\ x^2=0\text{ or }4x^2-32x+68=0 \\ \therefore x=0\text{ twice.} \\ \\ 4.\text{ Solve the other quadratic equation.} \\ 4x^2-32x+68=0 \\ \text{Applying the Quadratic Formula to solve this equation} \\ a=4,b=-32,c=68 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-(-32)\pm\sqrt[]{(-32)^2-4(4)(68)}}{2(4)} \\ \\ x=\frac{32\pm\sqrt[]{-64}}{8}=\frac{32\pm\sqrt[]{8^2*-1}}{8}=\frac{32\pm(\sqrt[]{-1}*\sqrt[]{8^2})}{8} \\ \\ \text{But }\sqrt[]{-1}=i \\ \\ x=(32\pm8i)/(8)=4\pm i \\ \\ \text{The solution to the quadratic equation }4x^4=32x^3-68x^2,\text{ is:} \\ x=0\text{ twice} \\ x=4+i \\ x=4-i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c9m91buwl7b2vjmmloyo61v2qpugcz0hd2.png)
Final Answer