Answer:
(a) 10π rad/s
(b) 58.98 in/s
(c) A point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).
Step-by-step explanation:
Part (a)
The angular speed w can be calculated as
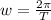
Where T is the period. So, replacing T = 2.00 x 10^-1 s, we get
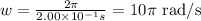
Then, the angular speed of the disk is 10π rad/s
Part (b)
The linear speed v is equal to
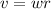
Where r is the radius. The radius is half the diameter, so the radius of a point on the rim of the disk will be 3.5 in/2 = 1.75 in. Then, the linear speed will be
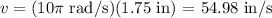
Therefore, the linear speed of a point on the rim of the disk is 54.98 in/s
Part(c)
The angular speed is equal to the angular displacement divided by the time. Since a point near to the centar have the same angular displacement as a point on the rim of the disk, the angular speed will be the same.
So, the answer is a point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).
Therefore, the answers are
(a) 10π rad/s
(b) 58.98 in/s
(c) A point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).