Question

Use the triangles to help answer part A,B and C

Answer 1

Given:

We have the two triangles:

ABC and ADC

Where:

AB = 10

AC = 8

Let's solve for the following:

• (a). Write a similiarity statement for the two similar triangles.

Two triangles are similar if their corresponding sides are in proportion.

To write a siiliarity statement, we have:

ΔABC ~ ΔADC

• (b). Let's find the length of BC.

To solve for BC, since ABC is a right traingle, apply Pythagorean Theorem:

`\begin{gathered} AB^2=AC^2+BC^2 \\ \\ BC^2=AB^2-AC^2 \\ \end{gathered}`

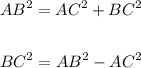
Where:

AB = 10

AC = 8

Thus, we have:

`\begin{gathered} BC^2=10^2-8^2 \\ \\ BC^2=100-64 \\ \\ BC^2=36 \\ \\ BC=√(36) \\ \\ BC=6 \end{gathered}`

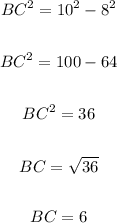
• (c). Let's find the length of CD.

Since they are similar triangles, the corresponding angles will be equal.

Thus, angle D = angle B = 36 degrees.

Now, apply the trigonometric ratio for tangent:

`tan\theta=(opposite)/(adjacent)`

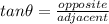
Where:

Opposite side = AC = 8 units

Adjcaent side = CD

Hence, we have:

`\begin{gathered} tan36=(8)/(CD) \\ \\ CD=(8)/(tan36) \\ \\ CD=(8)/(0.72654) \\ \\ CD=11 \end{gathered}`

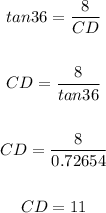
Therefore, the length of CD is 11 units.

ANSWER:

• (A). ,ΔABC, ~ ,ΔADC

• (B). 6 units

• (C). 11 units