Question

In a spin-the-wheel game, the is a 40% chance of the spinner landing on blue, a 10% chance of the spinner landing on red, and a 50% chance of the spinner landing on green. If the spinner lands on blue or green, there is a small prize. If the spinner lands on red, there is a lucky draw. The lucky involves picking a ball from a box that contains 15 yellow balls and 5 orange balls. A medium prize is won if a yellow ball is picked, and a laze prize is won if an orange ball is picked.a. Draw a tree diagram to represent all the possibles outcomes.b. Determine the probability of winning a small prize.c. Determine the probability of not winning a large prize.

Answer 1

Part A

We need to draw a tree diagram to represent all the possible outcomes.

For the spin, there are three initial possible outcomes (blue, green, and red). And if it lands on red, the third outcome becomes two other possible outcomes (yellow ball and orange ball).

There is a total of 20 balls (15 + 5).

Thus, given that it lands on red, the probability of picking a yellow ball is 15/20. And the probability of picking an orange ball is 5/20.

Therefore, we can draw the following diagram:

Answer

Part B

We need to determine the probability of winning a small prize.

We can see from the above diagram that it equals the sum of the probabilities of landing on blue and green:

`40\%+50\%=90\%=0.9`

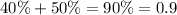
Answer: The probability of winning a small prize is 0.9.

Part C

We need to determine the probability of not winning a large prize.

One way of finding this probability is by finding the probability of winning a large prize and then subtracting it from the whole probability (1).

The probability of winning a large prize is the product of the probabilities of landing on red and of picking an orange ball?

`10\%\cdot(5)/(20)=(10)/(100)\cdot(5)/(20)=(50)/(2000)=(5)/(200)=0.025`

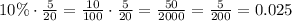
Therefore, the probability of not winning a large prize is given by:

`1-0.025=0.975`

Answer: The probability of not winning a large prize is 0.975.