Question

Solve the system graphically and check the solution. Y+5x=3. Y-X=6

Answer 1

The given system of equations is

`\begin{gathered} y+5x=3\rightarrow(1) \\ y-x=6\rightarrow(2) \end{gathered}`

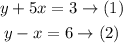
To solve it graphically, we have to draw each line, then take the point of intersection of them as a solution

To draw a line we need 2 points on it, then we will put a value of x, then find its corresponding value of y

For the 1st line:

Let x = 0

`\begin{gathered} y+5(0)=3 \\ y=3 \end{gathered}`

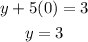
The first point is (0, 3)

Let x = 1

`\begin{gathered} y+5(1)=3 \\ y+5=3 \\ y+5-5=3-5 \\ y=-2 \end{gathered}`

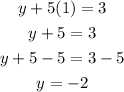
The second point is (1, -2)

For the 2nd line

Let x = 0

`\begin{gathered} y-0=6 \\ y=6 \end{gathered}`

The first point is (0, 6)

Let x = 1

`\begin{gathered} y-1=6 \\ y-1+1=6+1 \\ y=7 \end{gathered}`

The second point is (1, 7)

Let us draw the 2 lines

The green line represents equation (1)

The purple line represents equation (2)

The two lines intersected at point (-0.5, 5.5)

The solution of the system is (-0.5, 5.5)

To check the solution substitute x by -0.5 and y by 5.5, the answer must equal the right side

`\begin{gathered} 5.5+5(-0.5)=5.5-2.5=3 \\ \text{LHS}=\text{RHS} \end{gathered}`
`\begin{gathered} 5-5-(-0.5)=5.5+0.5=6 \\ \text{LHS}=\text{RHS} \end{gathered}`

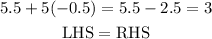
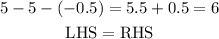
The solution satisfies both equations