Question

An ordinary (fair) coin is tossed 3 times. Outcomes are thus triples of "heads" () and "tails" () which we write , , etc. For each outcome, let be the random variable counting the number of tails in each outcome. For example, if the outcome is , then . Suppose that the random variable is defined in terms of as follows: . The values of are given in the table below.

Answer 1

Consider the table given below.

From the table above, the random value x of x are

`X(x)=-4,\text{ -2 and 4}`

To obtain the probability distribution for each value of x, we use the probability formula where,

`\text{Total outcome=8}`

For X(x)= -4, we have

`\begin{gathered} -4\text{ occurs thr}ee\text{ times, } \\ P_X(x)=\frac{\text{ number of occurence}}{Total\text{ outcome }} \end{gathered}`

Then

`P_X(-4)=(3)/(8)`

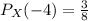
Also, for X(x)= -2, from the table we have

`\begin{gathered} -2\text{ occurs four times } \\ \text{Hence } \\ P_X(-2)=\frac{\text{ Number of occurence}}{total\text{ number}} \\ \\ \end{gathered}`

Then

`P_X(-2)=(4)/(8)=(1)/(2)`

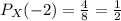
Similarly, value X(x)=4

4 occur once, hence

`\begin{gathered} P_x(x)=\text{ }\frac{\text{number of occurence}}{total\text{ outcome }} \\ \text{Then} \\ P_x(x)=(1)/(8) \end{gathered}`

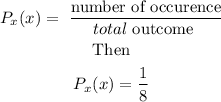
The solution is given in the image below: