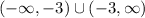Question

Find the domain of the rational function. f(x)=x−2/x+3Enter your answer in interval notation.

Answer 1

Given

The rational function,

`f(x)=(x-2)/(x+3)`

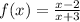
To find:

The domain of the rational function.

Step-by-step explanation:

It is given that,

`f(x)=(x-2)/(x+3)`

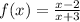
That implies,

Set the denominator equal to 0.

Then,

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

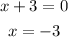
Therfore, the domain of the function is,

`\begin{gathered} Domain:\lbrace x\in R:x\\e-3\rbrace \\ \Rightarrow(-\infty,\infty)=R \\ \because x\\e-3 \\ \Rightarrow x\in(-\infty,-3)\text{ }or\text{ }(-3,\infty) \\ \Rightarrow x\in(-\infty,-3)\cup(-3,\infty) \end{gathered}`

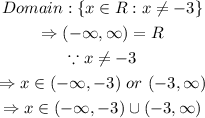
Hence, the interval notation of the domain is

`(-\infty,-3)\cup(-3,\infty)`