ANSWER
x = 3
Step-by-step explanation
We want to find the axis of symmetry of the quadratic equation given.
To do that, we have to first write the equation in the general form of a quadratic equation:
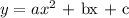
The given equation is:
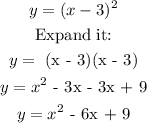
The axis of symmetry of a quadratic equation can be found as:
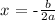
We have that:
b = -6
a = 1
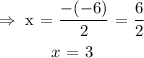
That is the axis of symmetry of the equation.