Question

4. Tyrell bought 4 pizzas and 5 subs and his bill was $56.25. Annabel bought 3 pizzas and 7 subs and her bill was $59.25. How much does each item cost?

Answer 1

let p represent pizza

let s represent subs

when he bought 4 pizza and 5 subs bill is $56.25

`4p\text{ + 5s = 56.25 --------1}`

when he bought 3 pizzas and 7 subs his bill is $59.25

`3p\text{ + 7s = 59.25}--------2`

solving the two equations simultaneosly

`\begin{gathered} 4p\text{ + 5s = 56.25 x 3 (multiply equation 1 by coefficient of p in equation 2 i.e 3)} \\ 3p\text{ + 7s = 59.25 x 4 ( multiply equation 2 by coefficient of p in eqaution 1 i.e 4)} \\ \text{these multiplications gives equation 3 and 4 below} \end{gathered}`
`\begin{gathered} 12p\text{ + 15s = 168.75 -------3} \\ 12p\text{ + 28s = 237}--------4 \\ \end{gathered}`
`\begin{gathered} \text{subtracting equation 3 from 4, p is eliminated and the equation below is obtained} \\ 13s\text{ = 68.25} \\ (i\mathrm{}e\text{ 12p - 12p) + (28s-15s) = 237-168.75)} \end{gathered}`

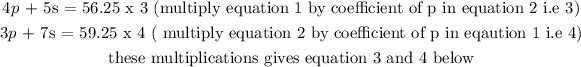
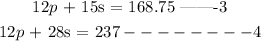
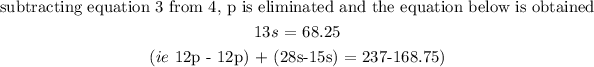
divide both side by 13

`\begin{gathered} (13s)/(13)=(68.25)/(13) \\ s\text{ = 5.25} \end{gathered}`

substitute s= 5.25 in equation 1

4p + 5(5.25) = 56.25

4p + 26.25 = 56.25

4p = 56.25 - 26.25

4p = 30

divide both side by 4

`\begin{gathered} (4p)/(4)=\text{ }(30)/(4) \\ p=7.5 \end{gathered}`

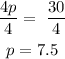
each pizza cost $7.5

each sub cost $5.25