We need to find the linear and the angular speeds of an object traveling around a circle.
The radius r of the circle is 3 feet. Thus, the perimeter p of the circle is:
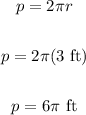
Also, we know that the object completes one full revolution every 5 seconds.
Thus, to find the linear speed V, we need to divide the number of feet it travels by the number of seconds it takes:
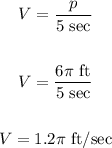
ow, tnotice that the complete revolution has 2π radians.
Then, to find the angular speed ω, we need to divide the number of radians it travels by the number of seconds it takes:
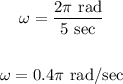
Therefore:
