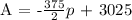Given:
a.) If the price of admission was $10, the attendance was about 1150 customers per day.
b.) When the price of admission was dropped to $6, attendance increased to about 1900 per day.
Let's generate the linear equation where:
x, y = p, A
m = slope
b = the y-intercept
We get,
Step 1: Let's determine the slope.
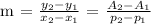
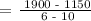
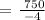

Step 2: Let's determine the y-intercept (b). Substitute p, A = 10, 1150 and m = -375/2 in A = mp + b
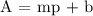
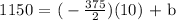
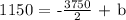
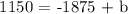
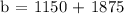
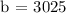
Step 3: Let's complete the equation. Substitute m = -375/2 and b = 3025 in A = mp + b
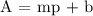
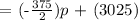
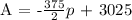
Therefore, the linear equation for the attendance in terms of the price, p, is: