Question

The speed of a moving bullet can be determined by allowing the bullet to pass throughtwo rotating paper disks mounted a distance75 cm apart on the same axle. From theangular displacement 33.9◦of the two bullet holes in the disks and the rotational speed1209 rev/min of the disks, we can determinethe speed of the bullet.33.9◦v1209 rev/min75 cmconroy (klc4842) – Homework 7, rotation 21-22 – dowd – (TorresLPHY1 3) 2What is the speed of the b

Answer 1

160.49 m /s

Step-by-step explanation:

We know that the angular speed of the disks is 1209 rev/min.

`\omega=1209\text{rev}/\min`

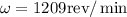
Let us convert this into degrees / s.

Now

1 rev = 360 degreees and 1 min = 60 s; therefore,

`\omega=(1209\cdot360^o)/(60s)`
`\boxed{\omega=7254^o/s\text{.}}`

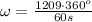
Now, we know that the angular separation of the holes in the two disks is 33.9 degrees. How long did it take the paper disk to rotate by this amount? The answer is

`33.9=(7254^o/s)t`

where t is the time needed.

Solving for t gives

`t=(33.9)/(7254)s`
`\boxed{t=4.67*10^(-3)s}`

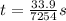
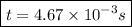
This means 4.67 * 10^-3 seconds passed before the bullet hit the second disk after hitting the first.

Now, we know that in those 4.67 * 10^-3 seconds, the bullet certainly travelled 75 cm = 0.75 m; therefore, its speed must be given by

`\begin{gathered} d=vt \\ \Rightarrow0.75=v(4.67\cdot10^(-3)s) \end{gathered}`

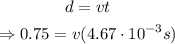
dividing both sides by 4.67 * 10^-3 s gives

`v=(0.75m)/(4.67\cdot10^(-3)s)`
`v=160.49m/s`

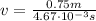
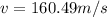
rounded to the nearest hundredth.

Hence, the velocity of the bullet (rounded to the nearest hundredth) is 160.49 m/s.