A soup company is looking at two designs for a new can. Can a have a diameter of 8 centimeters and a height of 15 centimeters. Can B has diameter of 10 centimeters and a height …

Question

asked May 17, 2023 216k views

1 Answer

Evyan · Answer 1 · 2023-05-23T20:24:45+0000

Given:

The diameter of can A is, d(A) = 8 cm.

The height of can A is, h(A) = 15 cm.

The diameter of can B is, d(B) = 10 cm.

The height of can B is, h(B) = 12 cm.

The objective is to find how much greater is volume of can B than can A.

Step-by-step explanation:

The general formula for volume of a can is,

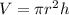
$V=\pi r^2h$

To find volume of A:

The volume of can A can be calculated as,

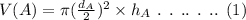
$V(A)=\pi((d_A)/(2))^2* h_A\text{ . . .. . .. (1)}$

On plugging the given values in equation (1),

$\begin{gathered} V(A)=3.14*((8)/(2))^2*15 \\ =753.6\operatorname{cm}^3 \end{gathered}$

To find volume of B:

The volume of can B can be calculated as,

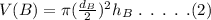
$V(B)=\pi((d_B)/(2))^2h_B\text{ . . . . .(2)}$

On plugging the given values in equation (2),

$\begin{gathered} V(B)=3.14*((10)/(2))^2*12 \\ =942\operatorname{cm}^3 \end{gathered}$

To find difference:

The difference between volume of can A and can B will be,

$\begin{gathered} V(B)-V(A)=942-753.6 \\ =188.4\operatorname{cm}^3 \end{gathered}$

Hence, the volume of can B is greater than can A by 188.4 cm³.