Given that
The cost for producing items is 40x + 300 and the revenue collected is 80x - 0.5x^2
And we have to write an equation for the profit and also we have to find the profit.
Explanation -
The profit is basically the difference between revenue and cost.
So the profit will be
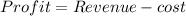
Substituting the values
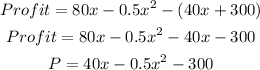
(a). The profit equation will be, P = 40x - 0.5x^2 - 300
(b). Here the profit given is $300 (P=300) and we have to find the values of x.
Then,
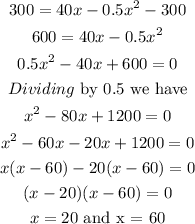
So the two values of x are 20 and 60.
(c). Now we have to check whether the profit can be $15000 or not.
For this, we have to put P = 15000 in the quadratic equation and if we get a solution for x then it is possible otherwise it is not.
So, substituting P = 15000
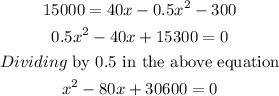
The solution to this equation is not possible. So Company cannot make a profit of $15000.
Hence the final answers are(a). P = 40x - 0.5x^2 - 300(b). 20 and 60(c). No