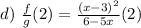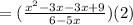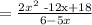Given f(x)=(x-3)^2 and g(x) = 6-5x
To find
a) (f+g)(2) = ( (x -3)^2 + 6-5x) (2) = ((x-3)(x-3) + 6 -5x) (2) = (x^2 -3x -3x + 9) (2) = (x^2 -6x +9 + 6-5x) (2)
= (x^2 -11x +15) (2) = 2x^2 -22x + 30
b) (f-g)(2) =( ( x-3)^2 -(6-5x)) (2) = ((x-3)(x-3) -6 +5x) (2) = ((x^2 -3x -3x +9) -6 + 5x) (2)
= (x^2 -6x +9 -6 +5x)(2)
= (x^2 -x +3)(2)
= 2x^2 -2x +6
c) (fg) (2) = (( x-3)^2) (6-5x) (2) = ( (x-3) (x-3) (6-5x) ) (2) = ( x^2 -3x -3x +9) (6-5x) (2)
= (x^2 -6x +9) (6-5x) (2) = ( x^2 -6x +9) (12 - 10x) = 12x^2 -72x +108 -10x^3 +60x^2 -90x
= 72x^2 -162x -10x^3 +108