EXPLANATION
Let's see the facts:
Revenue --> R(x) = 2sqrt (x) - 4 [x=number of items sold]
Cost --------> C(x) = 6 - sqrt (x)
The company will be profitable when the Revenue exceeds the cost.
Profitable condition: Revenue > Cost
Setting the two functions equal to each other and solving for x:
![2\sqrt[]{x}-4\text{ = 6 - }\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/osac609s09mi2ip1ibmgkz7o4ucaf9yt57.png)
Adding +sqrt(x) to both sides:
![2\sqrt[]{x}+\sqrt[]{x}-4\text{ = 6 }](https://img.qammunity.org/2023/formulas/mathematics/college/lee1ex2azodu9dkdhhl22mkqliwri07s7j.png)
Adding +4 to both sides:
![2\sqrt[]{x}+\sqrt[]{x}\text{ = 6 }+4](https://img.qammunity.org/2023/formulas/mathematics/college/zq7ospmqu4uwbzt65hcvdofnom1rir2v52.png)
Adding similar terms and simplifying:
![3\sqrt[]{x}=10](https://img.qammunity.org/2023/formulas/mathematics/college/s3ltm2i9rg81mcv56g5kmg3paztaojo0mo.png)
Dividing both sides by 3:
![\sqrt[]{x}=10/3](https://img.qammunity.org/2023/formulas/mathematics/college/2jzcmiqzmibxdfm4wwv9t9nsqowmao5wcd.png)
Applying the power of 2 to both sides:
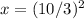
Simplifying:
x=11.11
The answer is about 111. In order for a company to be profitable, their revenue must exceed their cost. Setting the two functions equal to each other and solving for x gives the minimum number of items that need to be sold in order to be profitable. OPTION B.