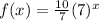Question

I’m currently doing my homework and really confused on this question. How would I be able to solve this.

Answer 1

We will have the following:

a) f(x) is a linear function:

We find the slope using the two points given:

`m=(70-10)/(2-1)\Rightarrow m=60`

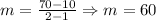
Now, we replace in the general formula for a linear function:

`y-y_1=m(x-x_1)\Rightarrow y-10=(60)(x-1)`
`\Rightarrow y-10=60x-60\Rightarrow y=60x-50`

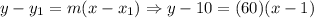
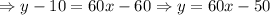
b) f(x) is a power function:

We know taht a power function is given by the general expression:

`f(x)=kx^n`

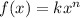
Now, we will have that for each point the following is true:

`\begin{cases}10=k(1)^n \\ \\ 70=k(2)^n\end{cases}`

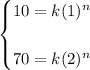
Now, we solve both for k and equal them:

`\begin{cases}k=(10)/(1^n) \\ \\ k=(70)/(2^n)\end{cases}\Rightarrow(10)/(1^n)=(70)/(2^n)\Rightarrow10\cdot2^n=70\cdot1^n`
`\Rightarrow\ln (10\cdot2^n)=\ln (70\cdot1^n)\Rightarrow\ln (10)+\ln (2^n)=\ln (70)+\ln (1^n)`
`\Rightarrow\ln (10)+n\ln (2)=\ln (70)+n\ln (1)\colon\ln (1)=0`

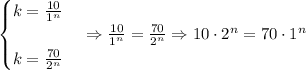
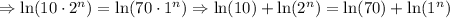
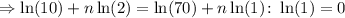
So:

`\ln (10)+n\ln (2)=\ln (70)+n\ln (1)\Rightarrow\ln (10)+n\ln (2)=\ln (70)`
`\Rightarrow n\ln (2)=\ln (70)-\ln (10)\Rightarrow n\ln (2)=\ln (70/10)`
`\Rightarrow n=(\ln (7))/(\ln (2))`

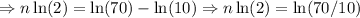
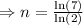
Now, we replace this value in one of the expressions and solve for k:

`10=k(1)^(\ln (7)/\ln (2))\Rightarrow k=10`

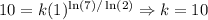
[1 at any power is also 1], now we write the expression that would be described:

`f(x)=10x^(\ln (7)/\ln (2))`

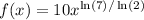
c) We remember that the general form of a exponential function is givven by:

`f(x)=a\cdot b^x`

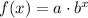
Now, using this and the two points we calculate:

`\begin{cases}10=a\cdot b^1 \\ \\ 70=a\cdot b^2\end{cases}`

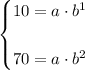
Now, we solve both for a and equal them:

`\Rightarrow\begin{cases}a=(10)/(b) \\ \\ a=(70)/(b^2)\end{cases}\Rightarrow(10)/(b)=(70)/(b^2)\Rightarrow10b^2=70b`
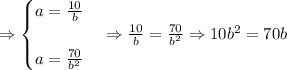
`\Rightarrow10b^2-70b=0\Rightarrow b=\frac{-(-70)\pm\sqrt[]{(-70)^2-4(10)(0)}}{2(10)}`
`\Rightarrow\begin{cases}b=0 \\ \\ b=7\end{cases}`

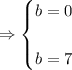
Now, since having a value of "b" equal 0 would make little sense, we work with b = 7. Then we replace in one of the expressions and solve for a, that is:

`\Rightarrow10=a\cdot7^1\Rightarrow7a=10\Rightarrow a=(10)/(7)`

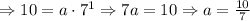
From this, we will have that the exponential form would be:

`f(x)=(10)/(7)(7)^x`