Question

I need to know how to solve solve the equation by factoring

Answer 1

Before we can factor the equation, let's convert first it into a general form of a quadratic equation ax² + bx + c = 0 where "x" is a variable. See the steps below.

Subtract 8b² and 2 on both sides of the equation.

`23b^2-49b+26-8b^2-2=8b^2+2-8b^2-2`

Arrange the terms in terms of their degree.

`23b^2-8b^2-49b+26-2=8b^2-8b^2+2-2`

Combine similar terms.

`15b^2-49b+24=0`

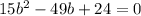
We have converted the equation into its general form and that is 15b² - 49b + 24 = 0.

Let's now factor this equation using the Slide and Divide Method.

1. Slide the leading coefficient 15 to the constant term 24 by multiplying them.

`15*24=360`

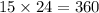
Upon sliding, the equation now becomes:

`b^2-49b+360=0`

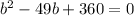
2. Let's find the factors of 360 that sums up to -49.

• 6 and 60 → sum is 66

,

• 8 and 45 → sum is 53

,

• 9 and 40 → sum is 49

,

• -9 and -40 → sum is -49

Therefore, the factors of 360 that sums to -49 are -9 and -40.

Hence, the equation b² - 49b + 360 can be factored into:

`(b-9)(b-40)=0`

3. Since we slide 15 earlier, divide the factors -9 and -40 by 15 by simplifying the fraction.

`-(9)/(15)\Rightarrow-(9/3)/(15/3)=-(3)/(5)`
`-(40)/(15)\Rightarrow-(40/5)/(15/5)=-(8)/(3)`

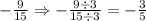
4. To find the factors of the equation, simply slide the denominator in each factor to b.

`\begin{gathered} (b-(3)/(5))\Rightarrow(5b-3) \\ (b-(8)/(3))\Rightarrow(3b-8) \end{gathered}`

The factors of the equation are (5b - 3)(3b - 8).

Let's now solve for b. Simply equate each factor to zero and solve for b.

`\begin{gathered} 5b-3=0 \\ 5b=3 \\ b=(3)/(5) \end{gathered}`
`\begin{gathered} 3b-8=0 \\ 3b=8 \\ b=(8)/(3) \end{gathered}`

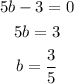
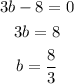
ANSWER:

The factors of the equation are (5b - 3)(3b - 8) and the values of b are 3/5 and 8/3.