Question

Use Descartes rule of signs to complete the chart with the possibilities for the nature of the roots of the equation:12x^5 -x^3 - 4x^2 +x -2=0

Answer 1

Given the equation:

`12x^5-x^3-4x^2+x-2=0`

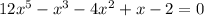
Using the Descartes rule of signs,

According to the Descartes rule, when the terms a single variable polynomial with real coefficients are ordered by descending variable exponents, the number of positive roots of the polynomial is either equal to the number of sign differences between consecutive non-zero coefficients, or is less than it by n even number.

In he avbove equation, the coefficients are

`12,\text{ -1, -4, 1, }`

Thus, there are two chnges. This implies that thereb are 2 or 0 positive real roots.

To find the number of negative roots, we substitute

`-x`

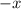
for x into the equation.

Thus, we have