We can make a drawing to see better:
7) We know that RM = 4 and MS = 9, so:
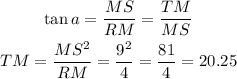
The answer is TM = 20.25
8) We know that RS = 20 and RM = 8, so:
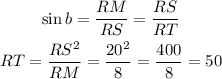
The answer is RT = 50.
9) We know that RM = 5 and MS = 7, so:
![\begin{gathered} \tan b=(RM)/(MS)=(RS)/(TS) \\ TS=RS\cdot(MS)/(RM) \\ RS=\sqrt[]{RM^2+MS^2} \\ TS=\sqrt[]{RM^2+MS^2}\cdot(MS)/(RM) \\ TS=\sqrt[]{5^2+7^2}\cdot(7)/(5)=\sqrt[]{25+49}\cdot(7)/(5) \\ TS=\sqrt[]{74}\cdot(7)/(5)\approx12.043 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/oa1j9496ypmt1x5u7rmo8af0gzcz2yyko4.png)
The answer is TS = 12.043
10) We know that RM = 1/2 and MS = 1/4, so:
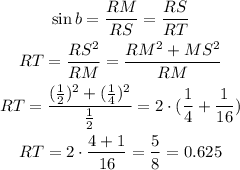
The answer is RT = 5/8 = 0.625