The general equation of a line is given by:
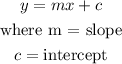
Given the line 2x -4y = -3
Step 1: Re-write the equation by making y the subject
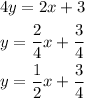
Since we have the equation of the line to be
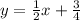
Step 2: Obtain the slope of this line
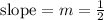
Step 3: Obtain the slope perpendicular to this line.
If two line are perpendicular, then
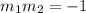
so that
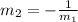
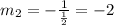
Hence the slope of the new line will be = -2
Step 4: Obtain the equation of the line using the formula:

where
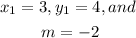
Thus,

=>

The equation of the line that s perpendicular to the line is
=> y= -2x +10
This can also be written in the form ax+by=c
as
Making the constant to be on the right-hand side and the variables to be on the left and side as shown below
Hence,
2x+y=10