Question

y = - (x + 3)2 + 5 Step 2: State the vertex: (h, k). Min. or Max. . value? (3.5) minimum value (8.5) maximum value AB, minimum value CA 6 animum value

Answer 1

The vertex form of a parabola is

`y=a(x-h)^2+k`

where the vertex is

`v=(h,k)`

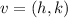
Now in our case, looking at our equation we see that h = -3 and k = 5; therefore, the coordinates of the vertex are

`(-3,5)`

Since the constant a = -1, the parabola is concave down, and therefore, the vertex is a maximum.

Hence, the correct answer is the fourth choice in the column.