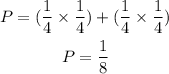A) Since there are a total of four qualifiers and we need to know the probability that 1 person wins both prizes, we will first find the probability of one person winning the first draw. That would be:
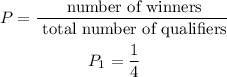
Now, since one person can be drawn again, the same would apply to the second prize:
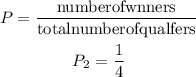
Therefore, the probability that one person wins both would be:
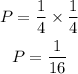
B) Next, we will find the probability that there will be 2 different winners. First, we find the probability of 1 person winning the prize:
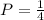
Then, the probability of another person winning the prize:
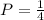
The probability of having 2 different winners would then be:
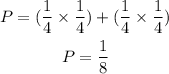
C) Now, the probability of Sofia winning at least one prize. The probability of winning at least 1 prize is equal to 1 - the probability of winning no prizes at all:
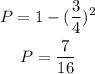
D) The answer for D would be the same for question A. Given that Frank is the one person who wins both prizes:
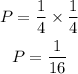
E) For E, this would be the same situation as B, given that the two different winners are Jake and Eldridge: