Question

Factor trinomials using the ‘ac’ method 9z^2 + 15z + 4

Answer 1

Hello there. To solve this question using the AC method, we'll have to remember some properties about factorizing numbers.

Given the trinomial:

`9z^2+15z+4`

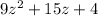
We start by labeling the numbers. The AC method requires that you find the A, B, C coefficients in:

`Ax^2+Bx+C`

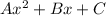
In this case, it is easy to see that:

`A=9,B=15,C=4`

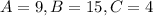
Now, we multiply A and C:

`A\cdot C=9\cdot4=36`

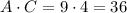
And we factorize this number in all the possible ways as a product of two numbers:

In the right column, you add the factors

And the numbers we'll choose are those that the sum is equal to B, in this case, 3 and 12 adds up to 15, that is the value of B we're looking for.

Now, we split the middle term in these factors:

`9z^2+3z+12z+4`

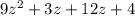
And we can factor some terms as follows:

`\begin{gathered} 3z\cdot(3z+1)+4\cdot(3z+1) \\ (3z+4)(3z+1) \end{gathered}`

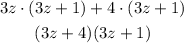
This is the factorization of this trinomial.