Question

cell phone company A charges a fee of $50 per month plus an additional $0.10 for every minute talked. Cell phone company B computes its monthly charge by using the equation y equals $0.05 x + $75 where y is the total cost and X is the number of minutes talked.which company has the greatest rate of change?

Answer 1

For company A

A monthly charge of $50 and an additional $0.10 for every minute talked can be represented by

y = 50 + 0.1x ------- equation 1

where y is the total cost and x is the number of minutes talked

For company B

The total cost is given by

y = 0.05 x + 75

=> y = 75 + 0.05x ---- equation 2

So, to determine the company with the greatest rate, let's substitute for different values of minutes

For company A

Let's find the derivative

`\begin{gathered} (d)/(dx)(50+0.01x) \\ \Rightarrow\text{ \$0.1} \end{gathered}`

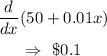
for company B

`\begin{gathered} (d)/(dx)(75+0.05x) \\ \Rightarrow\text{ \$0.05} \end{gathered}`

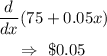
So, company A has the greatest rate of change at $0. 1