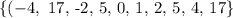Question

f(x) = x2 + 1 and g(x) = x2 - 1.Step 1 of 3: Find five ordered pairs that satisfy the function, f(x) = x2 + 1.AnswerHow to enter your answer (opens in new window){(1,0)(C).O.O.O).O.O.O.O.O.O)})C

Answer 1

Answer:
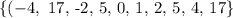
`\lbrace(-4,\text{ 17\rparen, \lparen-2, 5\rparen, \lparen0, 1\rparen, \lparen2, 5\rparen, 4, 17\rparen\textbraceright}`Step-by-step explanation:
`\begin{gathered} f(x)\text{ = x}^2\text{ + 1} \\ g(x)\text{ = x}^2-\text{ 1} \end{gathered}`

To get the ordered pairs that satisfy the function x, we will assign any value to x in order to get corresponding values of f(x).

Since there is no restriction on the values to assign to x from the question,

let x = -4, -2, 0, 2, 4

`\begin{gathered} when\text{ x = -4} \\ f(x)\text{ = \lparen-4\rparen}^2\text{ + 1} \\ f(x)\text{ = 16 + 1 = 17} \\ \\ when\text{ x = -2} \\ f(x)\text{ = \lparen-2\rparen}^2\text{ + 1} \\ f(x)\text{ = 4+ 1 = 5} \end{gathered}`
`\begin{gathered} when\text{ x = 0} \\ f(x)\text{ = 0}^2\text{ + 1} \\ f(x)\text{ = 0 +1 = 1} \\ \\ when\text{ x = 2} \\ f(x)\text{ = 2}^2\text{ + 1} \\ f(x)\text{ = 4+ 1 = 5} \\ \\ when\text{ x = 4} \\ f(x)\text{ = 4}^2\text{ + 1 } \\ f(x)\text{ = 16+ 1 = 17} \end{gathered}`

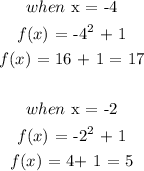
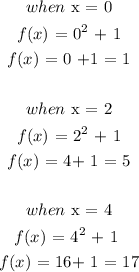
The ordered pair will be written in form: (x, f(x))

`\lbrace(-4,\text{ 17\rparen, \lparen-2, 5\rparen, \lparen0, 1\rparen, \lparen2, 5\rparen, 4, 17\rparen\textbraceright}`