Given:
The length of the copper wire is: l = 2.84 m.
The diameter of the copper wire is: d = 0.04 m.
The resistivity of the copper is: ρ = 1.7 x 10^-8 Ωm.
To find:
The resistance of the copper wire.
Step-by-step explanation:
The expression for the resistivity is given by:
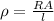
Here, A is the cross-sectional area of the copper wire, which is given by:
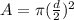
Substituting the value in the above equation, we get:
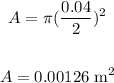
Rearrange the resistivity expression as:
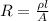
Substitute the values in the above equation, we get:
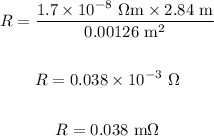
Final Answer:
The resistance of a copper wire is 0.038 milliOhms.