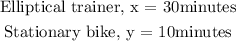Question

A gym has two machine you want to use. An elliptical trainer that burns 8 calories per minute and a stationary bike that burns 6 calories per minute. You have 40 minutes to exercise at the gym and you want to burn 300 calories total using both machines. How much time should you spend on each machine?( use x for the elliptical and y for the bike)Elliptical trainer x= Stationary bike y=

Answer 1

The first machine is 8 calories per minute.

The second machine is 6 calories per minute.

This allows us to set up a system of equations. The first equation will be for calories burned:

8x + 6y = 300.............1

'x' is minutes on the 8 calories per minute machine; 'y' is minutes on the 6 calories per minute machine.

A second equation simply shows that the total minutes add up to 40:

x + y = 40...................2

Now that we have two equations, we can solve them using the substitution method of the simultaneous equation.

`\begin{gathered} 8x+6y=300\ldots\ldots\ldots\text{.}.1 \\ x+y=40\ldots\ldots\ldots\ldots2 \end{gathered}`

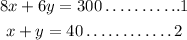
Isolate 'x' from equation 2

`x=40-y\ldots\ldots\ldots3`

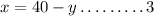
Substitute x = 40-y into equation 1

`\begin{gathered} 8(40-y)+6y=300 \\ 320-8y+6y=300 \\ 320-2y=300 \\ \text{Collect like terms } \\ 320-300=2y \\ 20=2y \\ \text{Divide both sides by 2} \\ (20)/(2)=(2y)/(2) \\ 10=y \\ \therefore y=10 \end{gathered}`

Now, substitute y = 10 into equation 3 and evaluate for x

`\begin{gathered} x=40-y \\ x=40-10=30 \\ \therefore x=30 \end{gathered}`

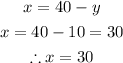
Hence, you should spend 30 minutes on machine 1 and 10 minutes on machine 2.

Final answers

`\begin{gathered} \text{Elliptical trainer, x = 30minutes} \\ \text{Stationary bike, y = 10minutes} \end{gathered}`