Question

Which equation could be used to solve for the measure of

Answer 1

Given in the question,

a.) △LMN

b.) ∠L is triple ∠M

c.) ∠N is double ∠M

From the given relationship, let's put them into an expression:

∠L is triple ∠M:

`\angle L\text{ = 3}\angle M`

∠N is double ∠M:

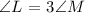
`\angle N\text{ = 2}\angle M`

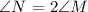
Let's recall that the sum of all interior angles of a triangle is 180°. Thus, in expression, we get:

`\angle L\text{ + }\angle M\text{ + }\angle N=180^(\circ)`

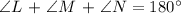
Substituting the equivalent ratio of ∠L and∠N with respect to ∠M, we get:

`\text{3}\angle M\text{ + }\angle M\text{ + 2}\angle M=180^(\circ)\text{ }\rightarrow\text{ }\angle M\text{ + 3}\angle M\text{ + 2}\angle M=180^(\circ)`

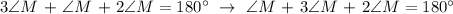
Therefore, the answer is letter A.