Question

A tank has a capacity of 13 gallons. When it is full, it contains 10% alcohol. How many gallons must be replaced with an 70% alcohol solution to give 13 gallons of 50% solution? Round your final answer to 1 decimal place if necessary.

Answer 1

Given:-

A tank has a capacity of 13 gallons. When it is full, it contains 10% alcohol.

To find how many gallons must be replaced with a 70% alcohol solution to give 13 gallons of 50% solution.

Let x denote the replaced solution containing 70 percent of alcohol.

S0 13-x contains 10% of alcohol.

Since 70 percent of alcohol contained in x. we get,

`(13-x)*(10)/(100)+x*(70)/(100)=13*(50)/(100)`

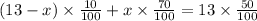
Now we simplify the above equation to get the required value of x. so we get,

`\begin{gathered} (13-x)(10)/(100)+x(70)/(100)=13*(50)/(100) \\ (13-x)*(1)/(10)+x(7)/(10)=13*(1)/(2) \\ (1)/(10)(13-x+7x)=(13)/(2) \\ (1)/(10)(13+6x)=(13)/(2) \\ 13+6x=(13*10)/(2) \end{gathered}`

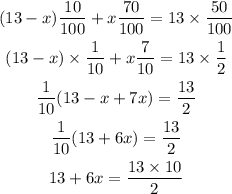
So by further simplifications. we get,

`\begin{gathered} 13+6x=(13*10)/(2) \\ 13+6x=65 \\ 6x=65-13 \\ 6x=52 \\ x=(52)/(6) \\ x=8.666 \end{gathered}`

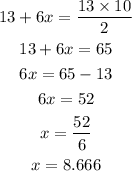
So the required value of gallons is approximately 8.7