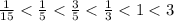Question

can you put these numbers on a number line from least to greatest please!!! 1/15, 1/5, 1/3, 3/5, 1, 3

Answer 1

To order fractions you have to look at their denominators, the grater it is, the smaller the fraction

So, for example

`\begin{gathered} (1)/(2)>(1)/(4)\text{ because 4>2} \\ \text{and} \\ (1)/(3)>(1)/(5)\text{ because 5>3} \end{gathered}`

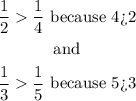
Next is when the numerator of the fraction has a number greater than 1, this means that it will be a higher number but still smaller than the integer.

For example

`(3)/(4)>(1)/(4)\text{because the numerator 3 is greater than 1}`

If the numerator is equal to the denominator, this means that the fraction is equal to a whole, for example:

`(5)/(5)=1`

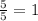
If the numerator is greater than the denominator, this means that the fraction is greater than one, for example

`\begin{gathered} \text{If }(3)/(3)=1 \\ \text{Then }(5)/(3)>1 \end{gathered}`

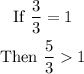
With all of this in mind, the greater values will be the "whole" numbers 3 and 1, next order the fractions, starting from the greaters denominators because those fractions correspond to the smaller values:

`(1)/(15)<(1)/(5)<(3)/(5)<(1)/(3)<1<3`