Question

Find the vertex coordinates for the following quadratic equation, writing solutions in decimal form:

Answer 1

We can find the vertex coordinates for this quadratic equation using the next formulas:

`x_v=-(b)/(2a),y_v=c-(b^2)/(4a)`

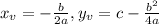
Where the values for a, b, c are obtained by looking at the values of these coefficients in the general quadratic expression:

`ax^2+bx+c`

Then, we have that:

a = 1, b = -3, c = -10.

Then, to find the x-coordinate of the quadratic equation, we have:

`x_v=-(-3)/(2\cdot1)=(3)/(2)\Rightarrow x_v=(3)/(2)=1.5`

To find the y-coordinate, we have:

`y_v=-10-((-3)^2)/(4\cdot1)=-10-(9)/(4)=(4\cdot(-10)-9)/(4)=(-40-9)/(4)=-(49)/(4)=-(48)/(4)-(1)/(4)`

Then:

`y_v=-(48)/(4)-(1)/(4)=-12-(1)/(4)=-12(1)/(4)=-12.25`

Therefore, the value for the y-coordinate is -12.25 (in decimal form).

In summary, we have that the vertex coordinates for the quadratic equation x²-3x-10 are (1.5, -12.25).